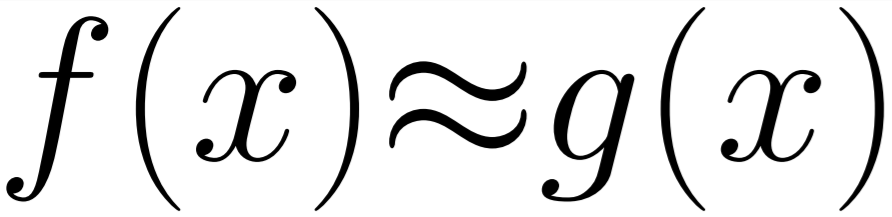Approximation is known win in many situations but it cannot be easily automatically performed in most systems. The approach is limited by a process we are calling the “three step approximation problem”.
The steps in the ‘three step approximation problem’ are:
Difficulty in identifying code that could be a target of approximation.
Performing a valid transformation.
Verifying that the transformed program is still valid.
Step 1: Finding Targets
Unstructured code and free functions can be used and combined in very complex ways. This makes it difficult to identify in large scale programs if any particular section of code is error tolerant.
There are tools such as automatic differentiation available but they require an understanding of the input range for the function to be able to give insight into error tolerance.
If we do consider a fixed input range and pattern of use for a function, then we can use fuzzing and differentiation to determine acceptable approximation ranges if any are possible. This is still a large problem as it will have to be applied for every possible level within an AST or similar program representation.
Step 2: Performing a Valid Transform
The literature on approximation is still quite light on what transformations work for which patterns. At the moment the whole field is relying on simple mathematical approximations.
For more progress in this area, we need to devise new methods to approximate code - and the method has to be able to be applied without human input.
Step 3: Validation
Once the potentially approximatable code has been transformed in some way it must then be validated in some kind of test. This means a robust look at the input to outputs when compared to the original function.
For some programs this testing can be trivial - such as those which rely on human visual error tolerances. For more mathematical problems it may be necessary to test every possible input, or a substantial enough sample to give confidence in the new solution.
Conclusion
These are the three steps we are looking to address in my PhD - we believe we have solutions for steps 1 and 2 - but step three is still relying on the same types of validation used in other imprecise software - such as those used for validating neural networks.