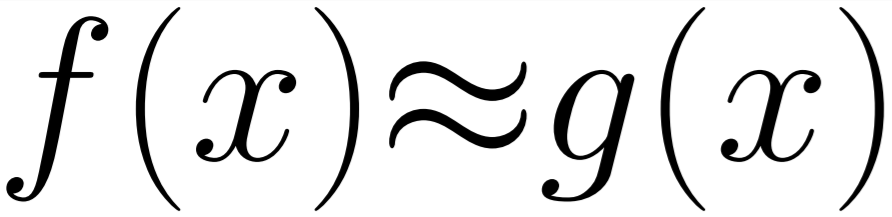So far in our approximation approaches we have been considering generating functions which match the input and out parameters of the function we want to optimise. In this post we will be considering two techniques which do not so directly follow this approach.
Regularisation
Is generally considered in mathematical modelling when we are looking to prevent overfitting or to solve the problem of modelling when the function is not a well-posed problem. In this context an ill-posed function is one that either:
Has no solution
The solution is not unique
or, the solutions behaviour doesn't change only on initial conditions.
When we are looking for an approximate function we are hoping that the function is ill-posed as we would ideally want the function solution to not be unique so we can find a better one!
In other articles we discussed the range of the function we are interested in, as well as the accuracy for each point in this range. In this section we are asking if there are discete points in the range that we care about more than others. For example, you might have some function in your application which takes some real number and returns it expensively mathematically altered in some fixed way - but you only call it in your application for the values of 0 or 1. In this instance we probably don't want to have the costly the calculation if the answer is either the result of f(0) or f(1). It might be cheaper to have a function which maps to those two results directly.
In this case for the case of only caring about those two results we can generate a "regularised" function that matches those requirements exactly.
These regularised functions can often be cheaper than the actual function as they only have to care about a specific set of points.
Relaxation
The next topic in the same vein is relaxation. Relaxation in the mathematical sense, more formally called "Integer Linear Programming Relaxation" is a technique for taking a program which has only integer solutions and allowing them to be expressed as real numbers to simplify the problem and then rounded back to integer numbers. This is known for its ability to take NP complexity programs and take them to P complexity (if that is of interest).
When we look at how this relaxation changes a problem we can see that it has the possibility to expand the total problem domain (by a range dependent on your rounding choice) and may not actually give the correct solution due to some constraints. Full details on the Mathematics and proofs for this can be found around Wikipedia.
For our use of it, we are looking at it for its ability to take a function given discrete results and model it as a continuous function. This allows us to approach some integer problems which are technically "infeasible" in an approximate manner - however, never optimally.
We can see approximate algorithms solving problems through this method if you look up the "Weighted Vertex Cover Problem" or similar shortest path or optimal distribution problems.
The book "Algorithms to Live By" contains some very good examples and explanations in the chapter covering this type of relaxation and lagrangian