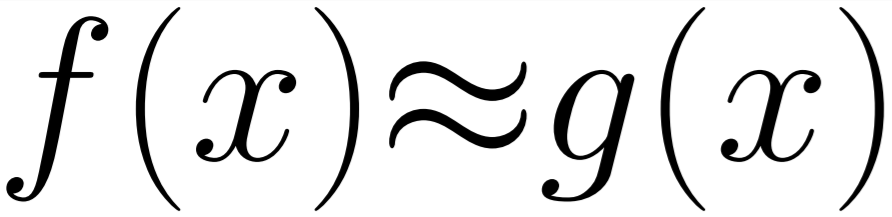One of the main factors when you are looking to approximate a function is understanding what part of the function you are approximating. Approximation is inherently a trade-off, so when we are approximating a function we may want to only approximate a certain part of it, or may want to approximate one section of the input to a higher accuracy than another.
But, before we can make any decisions on any of this we have to understand the full features of the function we want to approximate and a major feature of a lot of functions falls into the category of the "Radius of Convergence".
The most simple way to understand the "Radius of Convergence" is to consider y = ∑0.5x from 'x = 1' to 'x = infinity'. At x gets larger the result being added to the sum decreases. This causes the function to converge at y=1.
So if we were going to approximate this function by sampling it for various values of x, it would be quite wasteful for us to sample past x=10 as the function has fully converged then. This gives this function a radius of convergence of y= 1.9990. (This is quite fun to play with on WolframAlpha)
For a function which has convergence point (or points) it is important that we understand it so that we can increase the value of each point we sample and use in our own function generation. This gives us bounds and simplifies the work we have to do. Similar to how we can simplify intractable algorithms with priors, we can use this information to form our own "priors" in our generated functions.