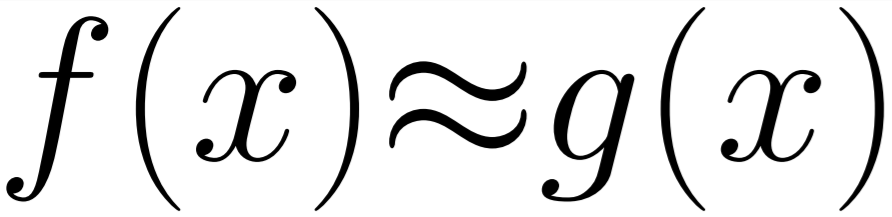In an earlier post we detailed a method to generate a function level cache which could be used to compare the input values to the function to past values in a cache so that we could return answers we had already calculated when the input values were near enough.
A large bottle neck in that method was that the input values and cache had to be manually searched and compared adding a significant overhead if the function it was mapping to was not significantly complex. It also meant that the choice of what to keep in the cache was difficult and expensive to manage.
Luckily, this problem is very similar to that normal cache behaviour - we can solve it with some clever hashing. We only want to look into the cache where we expect to find our similar data. The problem with hash functions is that they often try very hard to avoid collisions. In this circumstance we want to get collision, but only collisions when the input value to the hash function are similar.
For example, a simple hash function for a float value might be to simply return the integer representation binary for that float . It is a 1:1 mapping of address index to value, nice and simple. If we were instead to add 0.5f to the float and cast the float to an integer, effectively rounding to the nearest integer we would have a hashing function which was accurate only to within 1 unit. This means that 3.1, 3.4 and 2.7 would map to the same hash address - 3. Thus achieving an intentional cache collision and allowing us to not have to search through all of our cache for all possible values which are within one unit, we simply hash the input and if we have a value matching it in the cache we are good to go and if not we can continue without the cache and add it in afterwards for the next similar query to read.
As you might expect the implementation of this is relatively simple. Using Modern C++ we could implement this on using an std::unordered_map with the hash function overloaded for our type or passed in explicitly (see this example for an std::unordered_set).
However, we have our own requirements and constraints. Our map needs to have an explicit memory footprint and some type of ordering would be useful depending on the type of hashing we want to do as different functions have different relationships for their inputs and output, so some customisation is desired. As this is being written as a test, being able to explicitly add debug and control the flow without the complexity of overriding standard library functions is also a plus.
Therefore, it seems worthwhile to show a trivial implementation which can be expanded to meet our criteria and be used to more clearly express this idea. Also, its fun.
So, to begin with we have to think of what the constraints on our container are. If we want to match the behaviour of normal maps than we need a type for the key and a type for the data it is stores. In our case this will be the input type of the function we are caching and the output type of the result, respectively. Next, we want to be able to specify the number of entries allowed in the cache so that we can tweak the size for performance. And finally, we want to be able to specify the hash function so that we can correctly place inputs into nearby addresses. This gives us a class definition that looks something like this:
template<typename Key, typename T, unsigned int Size, unsigned int(*hashFunction)(T)> class CollidingHashTable { .... };
A little long winded, but it means we can statically declare a lot in the definition of the class.
(Side note: In this example we are only hashing for one input. This is for simplicity in this example. It would be possible to use variadics to allow for multiple inputs and storage to simplify the work of the programmer using the class - but its probably better to simply store all the inputs in a struct and use the type of that struct for simplicity in the code base. No point making it harder than it needs to be if you are probably going to change it later...)
Now that we have the vague definition for the class we need a definition for the structure which the input data will be held in.
In this step we need to think about what type of cache behaviour we would like as some of that behaviour will require information stored for each entry. In this example we have decided that I want the cache entries that are frequently accessed to stay in the cache as long as they are being used and some measure of their use for debug purposes. For debug, we probably also want to store the value that was used to generate the hash for that location also.
As a result we have four entries in our map entry class, two for usage and two for debug:
Storage Value : The value of the result of the function we are caching.
Hash Value: The value of the input to the function we are caching.
Hit Count: A running count of how many time this cache entry has been accessed.
Last Touch Index: The last time the cache entry was accessed (with the time being measured by a counter that increments every time the map performs an operation).
This gives code which looks like this:
struct HashEntry { HashEntry() { hits = 0; hashValue = -1; storageValue = -1; lastTouchIndex = 0; } T hashValue; T storageValue; unsigned int hits; unsigned int lastTouchIndex; };
Next, we need to define how our map is going to store the data and control information. In this case we have opted to use an std::array of our HashEntry with the size which we pass in during the creation of the map. We also need to store our operation index to use as a timer for determining how old information is in the cache, and an arbitrary value to decide the maximum time an object can be in the cache without being used to allow us to replace them efficiently.
With this extra information, our collision prone map should now look something like this:
template<typename Key, typename T, unsigned int Size, unsigned int(*hashFunction)(T)> class CollidingHashTable { public: CollidingHashTable() : m_lastOperationIndex(0), m_staleThreshold(Size) { } struct HashEntry { HashEntry() { hits = 0; hashValue = -1; storageValue = -1; lastTouchIndex = 0; } T hashValue; T storageValue; unsigned int hits; unsigned int lastTouchIndex; }; std::array<HashEntry, Size> m_table; unsigned int m_lastOperationIndex; unsigned int m_staleThreshold; };
To make this into a usable map class, we now have to add the insert and get functions.
The get is quite a trivial function, it simply takes the value, calculates a hash for it and then if an entry exists at that address returns the value and updates the hit count and last touch index of the entry.
The insert function has to handle a little bit more, it must handle if the value being passed in should be inserted into an empty position if it exists, or replace the current value that is being stored if that value is considered stale. It must also handle invalid inputs - this is important as we are specifying our own hash function and want to map the result of the hash function to the indices of our table. This can be changed to support any returned hash value (like an std::map) but it adds more complexity.
The code for these functions, with the rest, should look something like this:
template<typename Key, typename T, unsigned int Size, unsigned int(*hashFunction)(T)> class CollidingHashTable { public: CollidingHashTable() : m_lastOperationIndex(0), m_staleThreshold(Size) { } struct HashEntry { HashEntry() { hits = 0; hashValue = -1; storageValue = -1; lastTouchIndex = 0; } T hashValue; T storageValue; unsigned int hits; unsigned int lastTouchIndex; }; int Get(Key _hashValue, T& result) { m_lastOperationIndex++; unsigned int hash = hashFunction(_hashValue); if (m_table[hash].hits == 0) { return -1; } else { m_table[hash].hits++; result = m_table[hash].storageValue; m_table[hash].lastTouchIndex = m_lastOperationIndex; return 1; } } //Ret: 0-> Added, 1 -> Replaced, 2-> Occupied, -1 -> Error int Insert(Key _hashValue, T _storageValue) { //Increment the index of this operation and get the hash index. m_lastOperationIndex++; unsigned int hash = hashFunction(_hashValue); if (hash < 0 || hash >= Size) { return -1; } int returnVal = -1; //If the entry is empty or stale replace. if (m_table[hash].hits == 0) { returnVal = 0; } else if ((m_lastOperationIndex - m_table[hash].lastTouchIndex) > m_staleThreshold) { returnVal = 1; } else { return 2; } m_table[hash].storageValue = _storageValue; m_table[hash].hashValue = _hashValue; m_table[hash].hits = 1; m_table[hash].lastTouchIndex = m_lastOperationIndex; return returnVal; } std::string ToString() { std::string text; text.append("hashValue"); text.append(", "); text.append("storageValue"); text.append(", "); text.append("hits"); text.append(", "); text.append("lastTouchIndex"); text.append("\n"); for (int i = 0; i < Size; i++) { text.append(std::to_string(m_table[i].hashValue)); text.append(","); text.append(std::to_string(m_table[i].storageValue)); text.append(","); text.append(std::to_string(m_table[i].hits)); text.append(","); text.append(std::to_string(m_table[i].lastTouchIndex)); text.append("\n"); } return text; } std::array<HashEntry, Size> m_table; unsigned int m_lastOperationIndex; unsigned int m_staleThreshold; };
With this class altogether we can create a map like this:
CollidingHashTable< float, float, HASHTABLESIZE, SimpleHash> ourHashTable;
Where 'SimpleHash' is any hashing function we want.
As a simple example, here is the hashing function described above that is mapped for float inputs to a function in the range 0-20.
#define HASHTABLESIZE 20 unsigned int SimpleHash(float _in) { unsigned int intRep = (unsigned int)(_in+0.5f); unsigned int modVal = intRep % (HASHTABLESIZE-1); return intRep; }
And we can now test this by generating a cache of answers to the 'sqrt' function where it is accurate only to '+- 0.5f' of the input.
int SqrtAndStore(float _value, CollidingHashTable< float, float, HASHTABLESIZE, SimpleHash>& _table) { float sqrtVal = sqrt(_value); int res = _table.Insert(_value, sqrtVal); return res; } int main() { CollidingHashTable< float, float, HASHTABLESIZE, SimpleHash> ourHashTable; float testValues[] = { 2.f, 2.5f, 3.5f, 3.7f, 10.f, 19.f, 10.01f, 10.9f, 11.f, 11.4f }; for (int i = 0; i < 10; i++) { int res = SqrtAndStore(testValues[i], ourHashTable); if (res == 0) std::cout << "sqrt(" << testValues[i] << "): Added to empty hash index.\n"; if (res == 1) std::cout << "sqrt(" << testValues[i] << "): replaced what was at hash index.\n"; if (res == 2) std::cout << "sqrt(" << testValues[i] << "): hash was occupied so did nothing.\n"; if (res == -1) std::cout << "sqrt(" << testValues[i] << "): encountered an error in the hashing process.\n"; } std::cout << "\n" << ourHashTable.ToString(); return 0; }
This code and wrapping debug output will tell us the behaviour for each call to insert and print out the state of the cache so we can see how it behaved over the run. It should give you an output that looks like this:
sqrt(3.7): hash was occupied so did nothing. sqrt(10): Added to empty hash index. sqrt(19): Added to empty hash index. sqrt(10.01): hash was occupied so did nothing. sqrt(10.9): Added to empty hash index. sqrt(11): hash was occupied so did nothing. sqrt(11.4): hash was occupied so did nothing. hashValue, storageValue, hits, lastTouchIndex -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 2.000000,1.414214,1,1 2.500000,1.581139,1,2 3.500000,1.870829,1,3 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 10.000000,3.162278,1,5 10.900000,3.301515,1,8 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 -1.000000,-1.000000,0,0 19.000000,4.358899,1,6
As you can see by the resulting table we have successfully mapped results to the same hash locations based on value, but we have a lot of empty space in table. Ideally we would want to shape the size of the table and hash function to the function that is being called, but another alternative would be to extend this class to be able to switch the hash function being used in different conditions and reorder the information stored within. Alternatively we could have the cache resize up to a maximum size at the cost of a little computing, or behave like a standard std::map and have an index to data to allow all occupied cache entries to stored without any gaps to possibly get better cache coherence (if the additional small index doesn't overshadow the gain in a small table...). But that is all work for another day!
I hope this was helpful!
Additional Point: This method can be cheaply extended to converge on an average result in the range by adding a number of insertion attempts at the same hash and recording a sum of all the storage values and then when it is read from the cache return the sum divided by the number of entry attempts. This wont give you the average result of the function in the range covered by that cell but will give you the value weighted towards the most common insertion point - which is probably closer to the answer you are trying to get back.