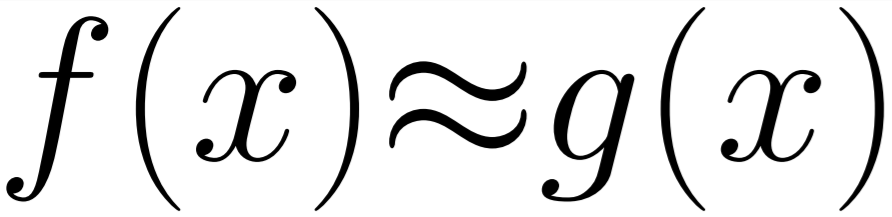In many modern applications we rely on the use of many multi-threaded algorithms, some of which are ran across CPUs and some of which are ran as GPGPU tasks.
For many types of programs this usually involves taking some task and splitting it into separate parts and recombining or processing the results of each separate part into a singular answer.
When each of separate threads executes correctly we are given the absolute correct answer in, hopefully, less time than if the task hadnt been separated into sub-components.
But what happens if one of the sub-components of the task failed? In most applications this would be a catastrophic error and we would end the program with no result. For a program which is doing a lot of heavy computation that could mean the loss of a whole lot of processed data.
To avoid that, it is possible to employ methods which detect a fault in a single sub-component and resubmit it for processing, exclude it from results or in some way handle the error and try and recover or nicely drop out of the program in a way that isn't too lossy.
However, what if the task we were running was made out of hundreds of thousands of components, where the result of executing each component could be predicted, modelled or in some way approximated from the input data and the results being produces by the other non-failing sub-components? In that situation we might be able to continue running the application by simply replacing the failed execution with an approximate answer and reporting to the program that it reported an error and give some statistical impact of that error. Such as up-to x% based on the number of sub-components and how many reported errors.
In that case you could run some work and have a work graph that looks like below.
In this new model that allows a failed/slow/broken task to be approximated from its input and neighbours we can add some stability to programs that don't require 100% accuracy and precision. If a program is fault-tolerant in its algorithms and results then it gives greater freedom to handle error or hardware problems which are guaranteed to occur on a long enough time scale.
Programs which allow for this condition are interesting in other ways too. If the program can handle up-to 10% error and still function and we have a task that is split into 1000 sub-tasks, and each sub-task is independent and side-effect free then we can manually add error into the program to increase performance if our approximation technique for failed sub-tasks is cheaper than the task that it was performing. This would give us an error that at worst within the threshold of error the program allows, and at best close to the correct answer.
In the case of artificially inducing error in the application we could reveal potential to reduce the power required by the computer to compute that tasks as well as improve the programs overall performance. We would want to induce this state in an application when the trade-off between accuracy and performance in non-linear, i.e. a small drop in accuracy gives a much more valuable benefit in another criteria.
There are many opportunities to use this technique in mobile computing, sensors and distributed computing as well as more general simulation technology to allow us to build better performing and more stable applications.